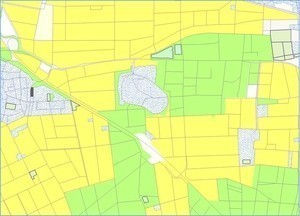
The program PUSH enables the automatic displacement of geo-objects of all kinds. The respective object characteristics, which influence the displacement, can be parameterized very flexibly. The results allow an automatic quality check. The program is also able to process larger data sets (e.g. map sheet topographic map 1:50,000).


This approach can be used to process point-shaped, line-shaped or surface-shaped objects. The coordinates of the object points are defined as unknown.
Various observations are introduced in the functional model:
- An observation class characterizes the objects themselves and describes the shape of the objects by the individual object's sides, angles, and orientation.
- Another important observation class is the distance between objects. If the distance values are below the specified minimum distance, the minimum distance is used as the target value. This results in the constraints that then have to be compensated.
- The coordinate unknowns are finally introduced as additional observations.
The stochastic model describes the accuracy situation: the object-specific observations are weighted highly, the distances receive either high weights (if minimum distance must be enforced) or low weights (if sufficient distance is available) depending on their size. The coordinates are generally given a low weighting, which allows any displacement of the objects that is required. However, it is important to be able to weight objects based on their type and thus generalize them. In such a way, objects can be specified as deformable or stiff (low or high weight of object-specific parameters), or as movable or fixed (low or high weight of object coordinates). These specifications can be made with regard to object classes, but also on the individual object level.
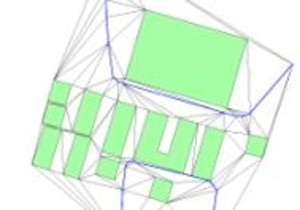
To determine the neighborhood of the objects, a triangulation of all objects is calculated, whereby it is forced that the object edges also represent triangular edges (Constrained Delaunay Triangulation). Objects are adjacent if they have a common triangle, which makes it very easy to determine their neighborhood. The most important control parameter in the overall process is the minimum object distance. In addition, you can specify whether objects should be deformable or fixed.
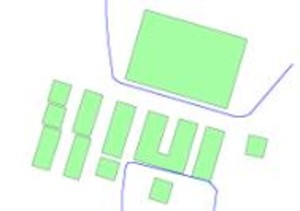
Example of displacement of buildings and roads








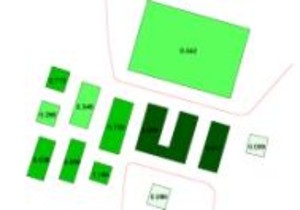


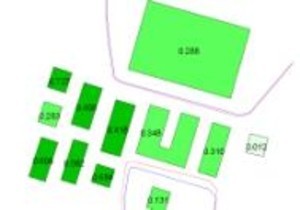


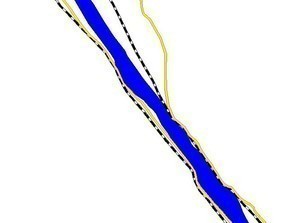
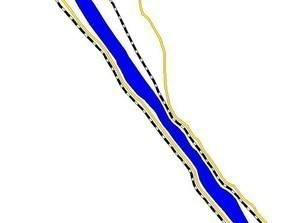
Typical generalization situation:
A river, flanked by roads and railways, is to be depicted on a smaller scale. The optimization method allows an automatic displacement of the objects against each other.




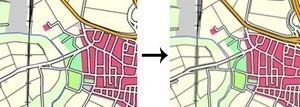
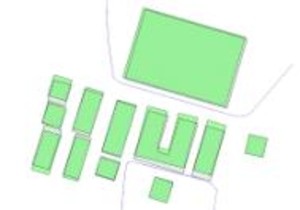
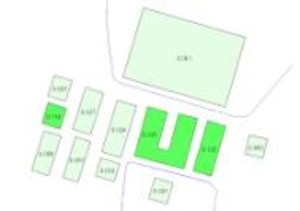
Integration of ALK data and ATKIS data
Due to the different scales of the two data sources (1:500 vs. 1:25,000), integration cannot be achieved by simple overlay alone. Therefore, the buildings are generalized first. The objects are then displaced against each other, with the road network assumed to be fixed. The figures below show the result of the generalization.
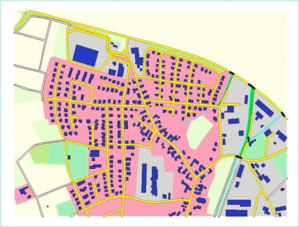


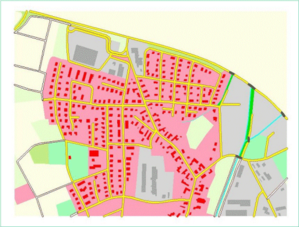


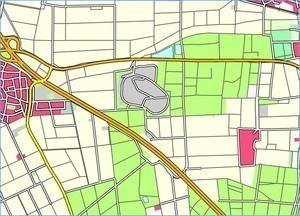
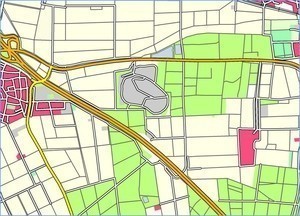
Example: Cartographic generalization of the DLM50
With PUSH it is possible to automatically resolve graphical conflicts in model-generalized DLM data.